POSTAL ASSISTANT EXAM MATERIAL- QUANTITATIVE APTITUDE-TIME & WORK
Disclaimer:- All the Information provided in this post are prepared & compiled by A. Praveen Kumar, SPM, Papannapet SO-502303, Telangana State for in good faith of Postal Assistant Exam Aspirants. Author of blog does not accepts any responsibility in relation to the accuracy, completeness, usefulness or otherwise, of contents.
Time and Work
1. Work from Days:
If A can do a piece of work in n days, then A's 1 day's work =
|
1
|
.
|
n
|
2. Days from Work:
If A's 1 day's work =
|
1
|
,
|
then A can finish the work in n days.
|
n
|
3. Ratio:
If A is thrice as good a workman as B, then:
Ratio of work done by A and B = 3 : 1.
Ratio of times taken by A and B to finish a work = 1 : 3.
4. No. of days = total work / work done in 1 day
5. Relationship between Men and Work
More men ------- can do -------> More work
Less men ------- can do -------> Less work
6. Relationship between Work and Time
More work -------- takes------> More Time
Less work -------- takes------> Less Time
7. Relationship between Men and Time
More men ------- can do in -------> Less Time
Less men ------- can do in -------> More Time
8. If M1 persons can do W1 work in D1 days and M2 persons can do W2 work in D2 days, then
9. If M1 persons can do W1 work in D1 days for h1 hours and M2 persons can do W2 work in D2 days for h2 hours, then
Note: If works are same, then M1D1h1 = M2D2h2
10. If A can do a work in ‘x’ days and B can do the same work in ‘y’ days, then the number of days required to complete the work if A and B work together is
11. If A can do a work in ‘x’ days and A + B can do the same work in ‘y’ days, then the number of days required to complete the work if A and B work together is
I think the single most useful formula for the topic Time and Work is
N1H1D1E1W2 = N2H2D2E2W1
Where:
N1 and N2 = number of person
H1 and H2 = Hours worked by per person per day (assumed constant)
D1 and D2 = days
E1 and E2 = Efficiency
W1 and W2= Amount of work done
1. A piece of work can be done by 16 men in 8 days working 12 hours a day. How many men are needed to complete another work, which is three times the first one,in 24 days working 8 hours a day. The efficiency of the second group is half that of the first group?
Solution –
N1H1D1E1W2 = N2H2D2E2W1
16*12*8*1*3 = N2*8*24*0.5*1
N2 = (16*12*8*1*3)/ (8*24*0.5*1) = 48
So number of men required is 48.
Note – you can remove anything from formula is not given in the question. For example if the question would have been –
2.“A piece of work can be done by 16 men in 8 days working 12 hours a day.How many men are needed to complete another work, which is three times the first one,in 24 days working 8 hours a day.”
The applicable formula would have been –
N1H1D1W2 = N2H2D2W1
Since nothing is mentioned about efficiency, we remove it from both sides.
1. Time taken to do a certain job by a certain number of workers
2. The change in the number of hours required to do a job if the number of workers is changed.
3. The number of hours required to do the job by different workers if their speeds are different.
4. Problems on wages earned by various workers executing a certain work in proportion with the amount of work done by each worker
5. Work done by various people in alternate intervals
6. Time taken by pipes/taps/leakages to fill/empty tanks/cisterns.
There are certain points that are to be kept in mind while doing problems. They are:-
1. A person does the same amount of work every day(unless specified in the problem).
Note
a. If A can do a piece of work in ‘n’ days, then the amount of work done by A in one day is 1/n.
b. Conversely, if A’s 1 day’s work=1/n, then A can finish the work in n days.
2. If there are more than one person involved carrying out the work collectively, it is assumed that the working capacity of each person is the same unless specified in the problem.
In general we can say that if w1 work is done by m1 men working h1 hours per day in d1 days and w2 work is done by m2 men working h2 hours per day in d2 days then
m1d1h1w2=m2d2h2w1
Generally, the following types of question are asked in examinations and here are few time work problems shortcuts
Types of Questions and usage of formulas
METHOD 1
M1 persons do a work in D1 days and M2 persons do the same work in D2 days then
we have the equation
M1*d1= M2* D2
METHOD 2
M1 persons can do W1 work in D1 days and M2 persons can do W2 work in D2 days then
we have (M1 D1)/W1 = (M2 D2)/W2
METHOD 3
if A can do a work in x days, B can do a work in y days then
A and B together (A+B) can do the same work in ( xy )/(x+y) days
METHOD 4
A alone can do a work in x days , A+B can do a work in y days then .
B alone can do the work in (xy)/(x-y)
METHOD 5
here A+B means A and B working together
if A working alone takes x days more than (A+B) and B working alone takes y days more than (A+B) then
the number of days taken by A and B together is given by
root of (xy)
METHOD 6
here A+B+C means A B C working together
A can do a work in x days , B can do the same work in y days , C can also do the same work in z days then
A+B+C can do the work in (xyz)/(xy+yz+zx) days
METHOD 7
here A+B+C means A B C working together
A+B can do a work in x days , B+C can do the work in y days, C+A can do the work in z days then
A+B+C can do the work in (2xyz )/xy+yz+zx days
METHOD 8
if x1 men or y1 women can reap the field in D days ,then
x2 men and y2 women take to reap it in D(x1y1)/(x2 y1+x1 y2) days
METHOD 9
a certain men can do a work in D days if there are x men less it could be finished in d days more, then
the no of men orginaly are x(D+d)/d
METHOD 10
a certain men can do a work in D days if there are x men more it could be finished in d days more,then
the no of men originally are x(D-d)/d
METHOD 11
if x1 men or x2 women or x3 boys can do a work in D days then
1 men + 1 women + 1 boy can do the same work in d(x1x2x3)/(x1x2+x2x3+x3x1)
1. A can do a work in 10 days. What is A’s 1 day work?
Sol: 1/10th of work
2. Two people can do a work in 10 days. What is 1 day 1 man work?
Sol: Since it is given as 2 people can do a work in 10 days, total work is 10 * 2 = 20 units of work.
Therefore, one day one man work = 1/total work = 1/20 units of work
3. Three men can do a work in 15 days. One man can do a work in how many days?
Sol: Since it is given as 3 people can do a work in 15 days, total work is 15 * 3 = 45 units of work.
Therefore, one man can complete the work in 45 days
4. One man one day work is 1/25. In how many days, can he finish the work?
Sol: Number of days required = 1/(1/25) = 25 days
5. A can work on 1km railway track in 1 day. In how many days, will he able to complete the work on 12km railway track?
Sol: no. of days = total work / work done in 1 day
Therefore, no. of days taken = 12/1 = 12 days
6. A can complete the work in 15 days. What fraction of work will be completed in 1 day?
Sol: Let the total work is 1 unit.
Work in 1day = total work/no. of days to complete
= 1/15th of work
7.A can do a piece of work in 3 days and B can do a piece of work in 5 days. In how many days will the work be completed if both A and B work together?
Sol:
Work done by A in 1 day = 1/3
Work done by B in 1 day = 1/5
Total work done by A and B in 1 day = 1/3 + 1/5 = 8/15
Therefore, no. of days to complete work by A and B together = 1/(Total work) = 1/(8/15) = 15/8 days which is less than 3 and 5
Using shortcut
Let us consider the total work be 15 units (LCM of 3 and 5)
So work done by A in 1 day = 15/3 = 5 units
Similarly work done by B in 1 day = 15/5 = 3 units
So total work done by A and B in 1 day = 5 + 3 = 8 units
Therefore, no. of days to complete total work i.e. 15 units = total work/work done in 1 day = 15/8 days
Note:
a. Work done by A and B in 1 day will always be greater than that of A and B individually
b. No. of days taken by A and B together will always be less than that of A and B individually
8.A can do a piece of work in 6 days, B can do a piece of work in 4 days and C can do a piece of work in 12 days. Find the no. of days to complete the work if A, B and C work together?
Sol:
Work done by A in 1 day = 1/6
Work done by B in 1 day = ¼
Work done by C in 1 day = 1/12
Total work done by A, B and C in 1 day = 1/6 + ¼ + 1/12 = 12/24 = 1/2
Therefore, no. of days to complete work by A, B and C together = 1/(Total work) = 1/(1/2) = 2 days which is less than 4, 6, 12
Using shortcut
Let us consider the total work be 24 units (LCM of 4, 6, 12)
So work done by A in 1 day = 24/4 = 6 units
work done by B in 1 day = 24/6 = 4 units
work done by C in 1 day = 24/12 = 2 units
So total work done by A, B and C in 1 day = 6 + 4 + 2 = 12 units
Therefore, no. of days to complete total work i.e. 24 units = total work/work done in 1 day = 24/12 = 2 days
9.A can do a piece of work in 6 days and B can do a piece of work in 12. Find the no. of days to complete the work if A and B work alternatively?
Sol:
Work done by A in 1 day = 1/6
Work done by B in 1 day = 1/12
Total work done by A and B working 1 day each = 1/6 + 1/12 = 3/12 = ¼
Therefore, 1/4th of work is done in 2days.
No. of days to complete total work if A and B work alternatively = 1/((1/4)/2) = 8 days
Using shortcut
Let us consider the total work as 12 units (LCM of 6, 12)
So work done by A in 1 day = 12/6 = 2 units
work done by B in 1 day = 12/12 = 1 unit
Total work done by A and B working 1 day each = 2 + 1 = 3 units in 2 days
Therefore, work done in 1 day = work/no. of days = 3/2 units
No. of days to complete work = total work/work in 1 day = 12/(3/2) = 8 days
10.30 men can complete a job in 40 days. Then 25 men can complete the same job in how many days?
Sol: As per the formula M1D1 = M2D2
30 * 40 = 25 * X = 30 * 40/25 = 48 days
11.30 men can complete 1500 units in 24 days working 6hrs a day. In how many days can 18 men can complete 1800 units working 8 hrs a day?
Sol: As per the formula M1D1h1/W1 = M2D2h2/W2
=> 30*24*6/1500 = 18*x*8/1800
=> x = 36 days
12. A and B can do a work in 10 and 15 days respectively. Then combined A & B, in how many days the work will be completed?
Sol: As per the formula x*y/(x + y)
A and B together can complete the work in 10 * 15/(10 + 15) = 6 days
A and B together can complete the work in 10 * 15/(10 + 15) = 6 days
13. A can do a work in 10 and, A and B together can do a work in 6 days. In how many days B can complete the same work?
Sol: As per the formula x*y/(x - y) B alone can complete the work in 10 * 6/(10 - 6) = 15 days
14. A is twice faster than B and B can complete in 12 days alone. Find the number of days to complete if A and B together work?
Sol: Given B works in 12 days
A is twice faster than B => A takes 2 times less time than B
Therefore, A completes work in 12/2 = 6 days
A and B together can complete in 12 * 6/(12 + 6) = 4 days
15. If 10 men or 18 boys can do a piece of work in 15 days, then 25 men and 15 boys together will do twice the work in:
Sol:10 men = 18boy hence 1 man = 18/10 boys
25 men + 15 boys = (25 * 18/10) + 15 = 60
now more work more days
more boys less days1 * 60 * x = 2*18*15 or x = (2*18*15)/60 = 9 days
25 men + 15 boys = (25 * 18/10) + 15 = 60
now more work more days
more boys less days1 * 60 * x = 2*18*15 or x = (2*18*15)/60 = 9 days
16.A is thrice as good a workman as B and takes 10 days less to do a piece of work than B takes. B alone can do the whole work in
Sol: Ratio of times taken by A and B = 1:3.
If difference of time is 2 days, B takes 3 days.
If difference of time is 10 days, B takes (3/2) * 10 =15 days.
If difference of time is 2 days, B takes 3 days.
If difference of time is 10 days, B takes (3/2) * 10 =15 days.
Sol: Let 1 mans 1 days work = x and 1 womens a days work = y
then 10x = 1/20 and 20y = 1/15 so x = 1/200 and y = 1/300
(5 men + 10 women)s 1 days work = (5/200) + 10/300 = 7/120.
So, they will finish the work in 120/7 = 17 and 1/7 days.
then 10x = 1/20 and 20y = 1/15 so x = 1/200 and y = 1/300
(5 men + 10 women)s 1 days work = (5/200) + 10/300 = 7/120.
So, they will finish the work in 120/7 = 17 and 1/7 days.
17.A is twice as good a workman as B and ‘together they complete a work in 15 days. In how many days can the work be completed by B alone
(As 1 days work):(Bs 1 days work) = 2: 1.
(A+B)s 1 day’s work= 1/15.
Divide 1/15 in the ratio 2 : 1
Bs 1 days work = (1/15) * (1/3) = 1/45
B alone can finish the work in 45 days.
(A+B)s 1 day’s work= 1/15.
Divide 1/15 in the ratio 2 : 1
Bs 1 days work = (1/15) * (1/3) = 1/45
B alone can finish the work in 45 days.
18. If Ramesh, Suresh and Harish can do a piece of work in 15 days, 10 days and 6 days respectiVelY how long will they take to do it, if all the three work at it together ?
(Ramesh + Suresh + Harish)S 1 days work = [(1/15) + (1/10) + (1/6)] = 10/3 =1/3
So, all the three will finish the work in 3 days.
So, all the three will finish the work in 3 days.
19.A and B can do a piece of work in 72 days, B and C can do it in 120 days. A and C can do it in 90 days. In what time can A alone do it?.
Sol: (A+B)s 1 days work = 1/72,
(B+C)s 1 days work = 1/120,
(A+C)s 1 days work= 1/90.
Adding 2(A+B+C)s 1 days work [(1/72) + (1/120) + (1/90)] = 12/360 = 1/30
(A+B+c)s 1 day’s work = 1/60.
As 1 days work = (1/60) - (1/120) = 1/120
A alone can fini the work in 120 days.
(B+C)s 1 days work = 1/120,
(A+C)s 1 days work= 1/90.
Adding 2(A+B+C)s 1 days work [(1/72) + (1/120) + (1/90)] = 12/360 = 1/30
(A+B+c)s 1 day’s work = 1/60.
As 1 days work = (1/60) - (1/120) = 1/120
A alone can fini the work in 120 days.
20. A does half as much work as B in three-fourth of the time. If together they take 18 days to complete the work, how much time shall B take to do
Sol: Suppose B takes x dáys to do the work.
A takes (2*(3/4)*x) = 3x/2 days to do it.
(A+B)s 1 days work= 1/18
1/x + 2/3x = 1/18 or x = 30.
A takes (2*(3/4)*x) = 3x/2 days to do it.
(A+B)s 1 days work= 1/18
1/x + 2/3x = 1/18 or x = 30.
21.45 men can complete a work in 16 days. Six days after they started working, 30 more men joined them. How many days will they now take to complete the remaining work?.
Sol: (45 * 16) men can complete the work in 1 day.
1 mans 1 days work = 1/720
45 mens 6 days work; = (1/16) * 6 = 3 / 8
Remaining work = (1 - (3/8)) = 5/8
75 mens 1 days work = 75/720 = 5/48
Now 5/48 work is done by them in 1 day.
5/8 work is done by them in (48/5) * (5x8) = 6 day
1 mans 1 days work = 1/720
45 mens 6 days work; = (1/16) * 6 = 3 / 8
Remaining work = (1 - (3/8)) = 5/8
75 mens 1 days work = 75/720 = 5/48
Now 5/48 work is done by them in 1 day.
5/8 work is done by them in (48/5) * (5x8) = 6 day
22. A and B can do a piece of work in 45 days and 40 days respectively. They began to do the work together but A leaves after some days and then B completed the remaining work in 23 days. The number of days after which A left the work was
Sol: (A+B)s 1 days work = (1/45) + (1/40) = 17/360.
Work done by B in 23 days =(1/40) * 23 =.23/40
remaining work = (1 — 23/40) = 17/40 .
Now, work was done by (A + B) in 1 day
17 /40 work was done by (A + B) in (1 * (360/17) * (17/40))= 9 days.
A left after 9 dáys.
Work done by B in 23 days =(1/40) * 23 =.23/40
remaining work = (1 — 23/40) = 17/40 .
Now, work was done by (A + B) in 1 day
17 /40 work was done by (A + B) in (1 * (360/17) * (17/40))= 9 days.
A left after 9 dáys.
23.4 men and 6 women finish a job in 8 days, while 3 men and 7 women finish it in 10 days. In how many days will 10 women working together finish it?
Sol: Let 1 mans 1 days work = x and 1 womans 1 days work = y.
Then, 4x + 6y = 1/8 and 3x+7y = 1/10
solving, we get y = 1/400
10 womens 1 day work = 10/400 = 1/40
10 women will finish the work in 40 days.
Then, 4x + 6y = 1/8 and 3x+7y = 1/10
solving, we get y = 1/400
10 womens 1 day work = 10/400 = 1/40
10 women will finish the work in 40 days.
24.12 children take 16 days to complete a work which can be completed by 8 adults in 12 days. 16 adults started working and after 3 days 10 adults left and 4 children joined them. How many days will it take them to complete the remaining work?
Sol: Let 1 child’s 1 day’s work = x and 1 adults 1 days work = y.
Then, 12x = 1/16 or x = 1/192 and 8y= 1/12 or Y = 1/196. Work done in 3 days = (16 * (1/96)*3)= 1/2
Work left = (1 - (1/2)) = 1/2
(6 adults + 4 children)s 1 days work = (6/96) + (4/192) = 1/12
1/12 work is done by them in 1 day.
1/2 work is done by them in (12 * (1/2)) = 6 days.
Then, 12x = 1/16 or x = 1/192 and 8y= 1/12 or Y = 1/196. Work done in 3 days = (16 * (1/96)*3)= 1/2
Work left = (1 - (1/2)) = 1/2
(6 adults + 4 children)s 1 days work = (6/96) + (4/192) = 1/12
1/12 work is done by them in 1 day.
1/2 work is done by them in (12 * (1/2)) = 6 days.
25. Twelve men can complete a work in 8 days. Three days after they started the work, 3 more men joined. In how many days will all of them together complete the remaining work?
Sol: 1 mans 1 days = 1/96
12 men’s 3 days work = (1/8) * 3 = 3/8.
Remaining work 1 — (3/8) = 5/8 15 mens 1 days work = 15/96
Now, 15/96 work is done by them in 1 day
5/8 work is done by them in (96/15) * (5/8) = 4 days
12 men’s 3 days work = (1/8) * 3 = 3/8.
Remaining work 1 — (3/8) = 5/8 15 mens 1 days work = 15/96
Now, 15/96 work is done by them in 1 day
5/8 work is done by them in (96/15) * (5/8) = 4 days
26. A can do of the work in 5 days and B can do of the work in 10 days. In how many days both A and B together can do the work?
Sol: Whole work will be done by A in (5 x 3) = 15 days.
Whole work will be done by B m (10 * (5/2)) = 25 days.
As 1 day’s work = 1/15 and Bs 1 days work = 1/25
(A+B)s 1 daYs work=((1/15) + (1/25) ) = 8/75
So, both together can finish it in 75/8 = 9 and 3/8 days days
Whole work will be done by B m (10 * (5/2)) = 25 days.
As 1 day’s work = 1/15 and Bs 1 days work = 1/25
(A+B)s 1 daYs work=((1/15) + (1/25) ) = 8/75
So, both together can finish it in 75/8 = 9 and 3/8 days days
27.A and B can do a Piece of work in 5 days ;B and c can do it in 7 day; A and C can do it in 4 days. Who among these will take the least time if put to do it alone?
Sol:(A+B)s 1 days work = 1/4
and (A+C)’s 1 day’s work = 1/4
2(A+B+C)s 1 days work = (1/5 + 1/7 + 1/4) = 83/140
(A+B+C)s 1 days work = 83/280
Cs 1 days work = (83/280 - 1/5) = 27/280
As 1 days work = (83/280 - 1/7) = 43/280
Bs 1 days work = (83/280 - 1/4) = 13/280
Thus time taken by A, B, C is 280/43 days, 280/13 days, 280/27 days respectively.
Clearly, the time taken by A is least.
and (A+C)’s 1 day’s work = 1/4
2(A+B+C)s 1 days work = (1/5 + 1/7 + 1/4) = 83/140
(A+B+C)s 1 days work = 83/280
Cs 1 days work = (83/280 - 1/5) = 27/280
As 1 days work = (83/280 - 1/7) = 43/280
Bs 1 days work = (83/280 - 1/4) = 13/280
Thus time taken by A, B, C is 280/43 days, 280/13 days, 280/27 days respectively.
Clearly, the time taken by A is least.
28. A does half as much work as B and C does half as much work as A and B together. If C alone can finish the work in 40 days, then together all will finish the work in:
Sol: C alone can finish the work in 40 days.
(A + B)can do it in 20 days
(A + B)s 1 days wok = 1/20.
As 1 days work : Bs 1 days Work = 1/2 : 1 = 1:2.
A’s 1 day’s work = (1/20) * (1/3) = (1/60). [Divide 1/20 in the raio 1:2] Bs 1 days work = (1/20) * (2/3) = 1/30
(A+B+c)S 1 day’s work = (1/60) + (1/30) + (1/40) = 9/120 = 3/40
All the three together will finish it in 40/3 = 13 and 1/3 days.
(A + B)can do it in 20 days
(A + B)s 1 days wok = 1/20.
As 1 days work : Bs 1 days Work = 1/2 : 1 = 1:2.
A’s 1 day’s work = (1/20) * (1/3) = (1/60). [Divide 1/20 in the raio 1:2] Bs 1 days work = (1/20) * (2/3) = 1/30
(A+B+c)S 1 day’s work = (1/60) + (1/30) + (1/40) = 9/120 = 3/40
All the three together will finish it in 40/3 = 13 and 1/3 days.
29. A, B and C can do a piece of work in 11 days, 20 days and 55 days respectively, working alone. How soon can the work be done if A is assisted by B and C on alternate days?
Sol: (A+B)s 1 days Work = (1/11) + (1/20) = 31/220
(A+C)S 1 days work = (1/11) + (1/55) = 6/55
Work done in 2 days = (31/220) + (6/55) = 55/220 = 1/4
Now, 1/4 work is done in 2 days.
Whole work will be done in (4 x 2) = 8 days.
(A+C)S 1 days work = (1/11) + (1/55) = 6/55
Work done in 2 days = (31/220) + (6/55) = 55/220 = 1/4
Now, 1/4 work is done in 2 days.
Whole work will be done in (4 x 2) = 8 days.
29. A can do a piece of work in 80 days. He works at it for 10 days and then B alone finishes the remaining work in 42 days. The two together could complete the work in
Sol: Work done by A in 10 days = (1/80) * 10 = 1/8
Remaining work=(1 — (1/8)) = 7/8
Now, 7/8 work is done by B in 42 days
Whole work will be done by B in 42 * (8/7) = 48 days.
As 1 days work = 1/80 and Bs 1 days work = 1/48
(A + B)’s 1 days work = [(1/80) + (1/48)] = 8/240 = 1/30
so, both will finish the work in 30 days.
Remaining work=(1 — (1/8)) = 7/8
Now, 7/8 work is done by B in 42 days
Whole work will be done by B in 42 * (8/7) = 48 days.
As 1 days work = 1/80 and Bs 1 days work = 1/48
(A + B)’s 1 days work = [(1/80) + (1/48)] = 8/240 = 1/30
so, both will finish the work in 30 days.
30.A and B can separately do a piece of work in 20 and 15 days respectively. They worked together for 6 days, after which B was replaced by C. If the work was finished in next 4 days, then the number of days in which C alone could do the work will be
Sol: (A + B)s 6 days work = 6 [(1/20) + (1/15)] = 7/20
(A+C)s 4days work = (3/10)*(A+C)s 1days work = 1/20 Cs 1 days work = (3/40) - (1/20) = 1/40
Hence, C alone can finish the work in 40 days.
(A+C)s 4days work = (3/10)*(A+C)s 1days work = 1/20 Cs 1 days work = (3/40) - (1/20) = 1/40
Hence, C alone can finish the work in 40 days.
31.A can do a piece of work in 7 days of 9 hours each and B can do it in 6 days of 7 hours each. How long will they take to do it, working together 8*(2/5) hours a day?
Sol:A can complete the work in (7 * 9) hrs = 63 hrs.
B can complete the work in (6 * 7) hrs = 42 hrs.
As 1 hours work = 1/63 and Bs 1 hours work = 1/42
(A+B)s 1 hours work = [(1/63) + (1/42)] = 5/126
Both will finish the work in (126/5) hrs
Number of days of8*(2/5) hrs each = (126/5) * (5/42) = 3 days.
B can complete the work in (6 * 7) hrs = 42 hrs.
As 1 hours work = 1/63 and Bs 1 hours work = 1/42
(A+B)s 1 hours work = [(1/63) + (1/42)] = 5/126
Both will finish the work in (126/5) hrs
Number of days of8*(2/5) hrs each = (126/5) * (5/42) = 3 days.
32. A father can do a job as fast as his two sons working together. If one son does the job in 3 hours and the other in 6 hours, how many hours does it take the father to do the job’?
Sol: Fathers 1 hours work= (1/3) + (1/6) = 1/2
Time taken by father to complete the work = 2 hours.
Time taken by father to complete the work = 2 hours.
33. A can do a piece of work in 15 days and B alone can do it in 10 days. B works at it for 5 days and then leaves. A alone can finish the remaining work in : .
Sol: Bs 5 days work = ((1/10) * 5) = 1/2
Remaining work = (1-(1/2)) = 1/2
A can do 1/2 work in 7and half days.
Remaining work = (1-(1/2)) = 1/2
A can do 1/2 work in 7and half days.
34. 12 men can complete a work in 18 days. Six days after they started working, 4 men joined them. How many days will all of them take to finish the remaining work?
Sol: (12 * 18) men can complete the work in 1 day.
1 mans 1 days work = 1/216
12 men’s 6 days work = (1/18)*6 = 1/3
remaining work = 1 - (1/3) = 2/3
16 mens 1 days work = 16/216 = 2/27
2/27 work is done by them in 1 day.
2/3 work is done by them in (27/2)*(2/3) = 9 days.
1 mans 1 days work = 1/216
12 men’s 6 days work = (1/18)*6 = 1/3
remaining work = 1 - (1/3) = 2/3
16 mens 1 days work = 16/216 = 2/27
2/27 work is done by them in 1 day.
2/3 work is done by them in (27/2)*(2/3) = 9 days.
35. A and B can together finish a work in 30 days. They worked at it for 20 days and then B left. The remaining work was done by A alone in 20 more days. A alone can finish the work in:.
Sol: Work done by A and B in 20 days = (1/30 * 20) = 2/3
Remaining work= ( 1 -2/3) = 1/3 Now,1/3 work is done by A in 20days
Whole work will be done by A in (20x3) = 60 days.
Remaining work= ( 1 -2/3) = 1/3 Now,1/3 work is done by A in 20days
Whole work will be done by A in (20x3) = 60 days.
36. A can do a piece of work in 30 days while B alone can do it in 40 days. In how many days can A and B working together do it?
Sol:As l days work = 1/30 and Bs l days work= 1/40
(A + B)s 1 days work = (1/30 + 1/40) = 7/120
Both together will finish the work in 120/7 = 17.14 days.
(A + B)s 1 days work = (1/30 + 1/40) = 7/120
Both together will finish the work in 120/7 = 17.14 days.
37. A piece of work can be done by 6 men and 5 women in 6 days or 3 men and 4 women in 10 days. It can be done by 9 men and 15 women in
Sol: Let 1 mans 1 days work =x and 1 womans 1 days work = y. Then, 6x+5y = 1/6 , 3x+4y = 1/10
On solving, we get x = 1/54 and y = 1/90
(9 men + 15 women)s 1 days work = (9/54) + (15/90) = 1/3
They will finish the work in 3 days.
On solving, we get x = 1/54 and y = 1/90
(9 men + 15 women)s 1 days work = (9/54) + (15/90) = 1/3
They will finish the work in 3 days.
38. A can do a certain job in 25 days which B alone can do in 20 days. A started the work and was joined by B after 10 days. The number of days taken in completing the work was
Sol: Work done by A in l0 days = (1/25) *10 = 2/5.
Remaining work = 1 - (2/5) = 3/5
(A+B)s 1 days work = (1/25) + (1/20) = 9/100
9/100 work is done by them in 1 day.
hence 3/5 work will be done by them in (100/9) * (3/5) = 20/3days.
Total time taken = (10 + 20/3) = 16 * (2/3) days.
Remaining work = 1 - (2/5) = 3/5
(A+B)s 1 days work = (1/25) + (1/20) = 9/100
9/100 work is done by them in 1 day.
hence 3/5 work will be done by them in (100/9) * (3/5) = 20/3days.
Total time taken = (10 + 20/3) = 16 * (2/3) days.
39.Ram can do a piece of work in 8 days which Shyam can finish in 12 days. If they work at it on alternate days with Ram beginning, in how many days, the work will be finished?.
Sol: (Ram + Shyam)s 2 days work = (1/8) + (1/12) = 5/24
Their 8 days work = (5/24) * 4 = 5/6
Their 8 days work = (5/6) + (1/8) = 23/24
Remaining work = (1 - (23/24))
Now it is Shyam’S turn.
1/12 work is done by him in 1 day.
1/24 work is done by him in (12 * (1/24)) = 1/2 day.
Total time taken = 9 and half days.
Their 8 days work = (5/24) * 4 = 5/6
Their 8 days work = (5/6) + (1/8) = 23/24
Remaining work = (1 - (23/24))
Now it is Shyam’S turn.
1/12 work is done by him in 1 day.
1/24 work is done by him in (12 * (1/24)) = 1/2 day.
Total time taken = 9 and half days.
40. A, B and C are employed to do a piece of work for Rs. 529. A and C are supposed to finish 19/23 of the work together. How much shall be paid to B ?
Sol: Work done by B = 1 - (19/23) = 4/23
(A + C) : B = (19/23) : (4/23) = 19:4
Bs share = RS.529*(4/23) = 92
(A + C) : B = (19/23) : (4/23) = 19:4
Bs share = RS.529*(4/23) = 92
41. A can do a certain job in 12 days. B is 60% more efficient than A. The number of days, it takes B to do the same piece of work, is.
Ratio of times taken by A and B = 160:100 = 8:5
8 : 5 :: 12 : x or 8x = 5*12 or x = 7 and half days.
8 : 5 :: 12 : x or 8x = 5*12 or x = 7 and half days.
42. A and B together can complete a piece of work in 35 days while A alone can complete the same work in 60 days. B alone will be able to complete the same work in:
Sol:(A+B)s 1 days work = 1/35 and As 1 days work = 1/60
Bs 1 days work =(1/35 - 1/60) = 5/420 = 1/84 |
43.A man can do a piece of work in 5 days, but with the help of his son, he can do it in 3 days. In what time can the son do it alone?
Son's 1 day's work
|
= (1/3-1/5)
|
=2/15.
| |
The son alone can do the work in
|
= 15/2
|
=7x1/2 days.
|
44.Sakshi can do a piece of work in 20 days. Tanya is 25% more efficient than Sakshi. The number of days taken by tanya to do the same piece of work is
Ratio of times taken by Sakshi and Tanya=125:100
| ||
= 5 : 4.
| ||
Suppose Tanya takes x days to do the work.
| ||
5 : 4 ::20 : x
| ||
x<=> (4×20/5)
| ||
<=> 16 days.
|
45.Kim can do a work in 3 days while David can do the same work in 2 days. Both of them finish the work together and get Rs.150. What is the share of Kim?
Kim's wages : David's wages
|
= Kim's 1 day's work : David's 1 day's work
|
= 1/3 : 1/2
| |
= 2 : 3
| |
Kim's share
|
= Rs.(2/5×150)
|
=Rs.60.
|
Courtesy : http://akulapraveen.blogspot.in/
POSTAL ASSISTANT EXAM MATERIAL- QUANTITATIVE APTITUDE-NUMBER SYSTEM
Disclaimer:- All the Information provided in this post are prepared & compiled by A. Praveen Kumar, SPM, Papannapet SO-502303, Telangana State for in good faith of Postal Assistant Exam Aspirants. Author of blog does not accepts any responsibility in relation to the accuracy, completeness, usefulness or otherwise, of contents.
NUMBER SYSTEM-1
DOWNLOAD BY CLICKING THE BELOW LINK
Numeral: In Hindu Arabic system, we use ten symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 called digits to represent any number.
A group of digits, denoting a number is called a numeral.
TYPES OF NUMBERS
1. Natural Numbers: Counting numbers 1, 2, 3, 4, 5,….. are called natural numbers.
2. Whole Numbers: All counting numbers together with zero form the set of whole numbers. Thus,
(i) 0 is the only whole number which is not a natural number.
(ii) Every natural number is a whole number.
3. Integers: All natural numbers, 0 and negatives of counting numbers i.e., {…, -3,-2,-1, 0, 1, 2, 3,…..} together form the set of integers.
(i) Positive Integers: {1, 2, 3, 4, …..} is the set of all positive integers.
(ii) Negative Integers: {- 1, – 2, – 3,…..} is the set of all negative integers.
(iii) Non-Positive and Non-Negative Integers: 0 is neither positive nor negative. So, {0, 1, 2, 3,….} represents the set of non-negative integers, while {0, -1,-2,-3,…..} represents the set of non-positive integers.
4. Even Numbers: A number divisible by 2 is called an even number, e.g., 2, 4, 6, 8, 10, etc.
5. Odd Numbers: A number not divisible by 2 is called an odd number. e.g., 1, 3, 5, 7, 9, 11, etc.
6. Prime Numbers: A number greater than 1 is called a prime number, if it has exactly two factors, namely 1 and the number itself.
Prime numbers up to 100 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Prime numbers Greater than 100: Let p be a given number greater than 100.
To find out whether it is prime or not, we use the following method :
Find a whole number nearly greater than the square root of p. Let k > *jp. Test whether p is divisible by any prime number less than k. If yes, then p is not prime. Otherwise, p is prime.
e.g,, We have to find whether 191 is a prime number or not. Now, 14 > V191.
Prime numbers less than 14 are 2, 3, 5, 7, 11, 13.
191 is not divisible by any of them. So, 191 is a prime number.
7. Composite Numbers: Numbers greater than 1 which are not prime, are known as composite numbers, e.g., 4, 6, 8, 9, 10, 12.
Note:
(i) 1 is neither prime nor composite.
(ii) 2 is the only even number which is prime.
(iii) There are 25 prime numbers between 1 and 100.
8. Co-primes: Two numbers a and b are said to be co-primes, if their H.C.F. is 1. e.g., (2, 3), (4, 5), (7, 9), (8, 11), etc. are co-primes
Basic Formulas:
1. (a + b)2 = a2 + b2 + 2ab
2. (a – b)2 = a2 + b2 – 2ab
3. (a + b)2 – (a – b)2 = 4ab
4. (a + b)2 + (a – b)2 = 2 (a2 + b2)
5. (a2 - b2) = (a + b) (a – b)
6. (a + b + c)2 = a2 + b2 + c2 + 2 (ab + bc + ca)
7. (a3 + b3) = (a +b) (a2 – ab + b2)
8. (a3 – b3) = (a – b) (a2 + ab + b2)
9. (a3 + b3 + c3 -3abc) = (a + b + c) (a2 + b2 + c2 – ab – bc – ca)
10. If a + b + c = 0, then a3 + b3 + c3 = 3abc.
Natural numbers (Positive integers) : 1, 2, 3, 4,....
Whole numbers (Non-negative integers) : 0, 1, 2, 3,....
Negative integers: − 1, − 2, − 3,....
Integers: ...., −2, − 1, 0,1, 2,.....
Even numbers: ...., − 2, 0, 2, 4,.... (2n)
Odd numbers: ....., −3, −1,1, 3,... (2n + 1)
Prime numbers (exactly 2 factors) : 2, 3, 5, 7, 11,....
Composite numbers (more than 2 factors) : 4, 6, 8, 9,10,....
Perfect numbers (Sum of all the factors is twice the number) : 6, 28, 496, ..
Co-primes (relative primes) (Two numbers whose HCF is 1) : 2 & 3, 8 & 9,..
Twin primes (Two prime numbers whose difference is 2) : 3 & 5, 5 & 7,.
Rational numbers (qp form, p & q are integers, q ≠ 0 ) : 32, 23 , 2, 0.5,..
Irrational numbers (which cannot be represented in the form of a fraction)
:2, 35, e, π , 0.231764735...)
:2, 35, e, π , 0.231764735...)
Decimal Numbers: 0.2, 1.25, 0.3333….
Terminating Decimal Numbers (which terminates): 0.23, 2.374, ….
Non Terminating Decimal Numbers (Which doesn’t terminate): 0.33…., 0.121212…, 0.2317…
Pure Recurring Decimals (All the figures after decimal point repeats) : 0.33…., 0.121212…
Mixed Recurring Decimals (Some figures after decimal repeats): 0.245555…, 0. 2343434…
Pure recurring decimal to fraction conversion
Ex. 0.ababab ….. = 99ab
Mixed recurring decimal to fraction conversion
Ex. 0.abcbcbc … = 990aabc−
→ 1 is the neither prime, nor composite.
→ 2 is the only even prime.
→ If x & y are two integers, then (x + y) ! is divisible by x !. y!
→ The product of ‘n’ consecutive numbers is divisible by n!.
→ (xn + yn) is divisible by (x + y), when n is an odd number.
→ (xn – yn) is divisible by (x + y)(x – y), when n is an even number.
→ (xn – yn) is divisible by (x – y), when n is an odd number.
→ 2 is the only even prime.
→ If x & y are two integers, then (x + y) ! is divisible by x !. y!
→ The product of ‘n’ consecutive numbers is divisible by n!.
→ (xn + yn) is divisible by (x + y), when n is an odd number.
→ (xn – yn) is divisible by (x + y)(x – y), when n is an even number.
→ (xn – yn) is divisible by (x – y), when n is an odd number.
9. Some Important points:
→ Every number ‘N’ can be written as N = ap × bq × cr …. . (a, b, c,…. are prime numbers.)
→ If p, q, r ……. are even, ‘N’ is a perfect square.
→ If p, q, r are multiples of 3, ‘N’ is a perfect cube.
→ Number of factors of N = (p+ 1) (q + 1) (r + 1) …..
→ Sum of the factors of N = ((a^(p+1)-1)/(a-1))((b^(q+1)-1)/(b-1)).........
→ Number of co – primes of ‘N’ , which are less than N = N (1 – 1/a) (1 – 1/b)….
→ Sum of these co-primes = N/2 × N (1 – 1/a) (1 – 1/b)….
→ Numbers of ways of writing ‘N’ as a product of 2 co-primes = 2 n – 1 , n is the number of different prime numbers in ‘N’
→ If n is a prime number, (n –1)! +1 is divisible by n.
→ If n is a natural number and p is a prime number, then (np –n) is divisible by p
→ The last digit of the powers of 2,3,7,8 repeats after every 4th power.
→ The last digit of any power of 0,1, 5,6 is always 0,1,5, 6 respectively.
→ The last digit of the powers of 4 and 9 repeats after every 2nd power.
→ The last two digits of any number is the remainder obtained by dividing that number by 100.
- Decimal Fractions:
Fractions in which denominators are powers of 10 are known as decimal fractions.
Thus,
|
1
|
= 1 tenth = .1;
|
1
|
= 1 hundredth = .01;
|
10
|
100
|
99
|
= 99 hundredths = .99;
|
7
|
= 7 thousandths = .007, etc.;
|
100
|
1000
|
- Conversion of a Decimal into Vulgar Fraction:
Put 1 in the denominator under the decimal point and annex with it as many zeros as is the number of digits after the decimal point. Now, remove the decimal point and reduce the fraction to its lowest terms.
Thus, 0.25 =
|
25
|
=
|
1
|
; 2.008 =
|
2008
|
=
|
251
|
.
|
100
|
4
|
1000
|
125
|
- Annexing Zeros and Removing Decimal Signs:
Annexing zeros to the extreme right of a decimal fraction does not change its value. Thus, 0.8 = 0.80 = 0.800, etc.
If numerator and denominator of a fraction contain the same number of decimal places, then we remove the decimal sign.
Thus,
|
1.84
|
=
|
184
|
=
|
8
|
.
|
2.99
|
299
|
13
|
- Operations on Decimal Fractions:
- Addition and Subtraction of Decimal Fractions: The given numbers are so placed under each other that the decimal points lie in one column. The numbers so arranged can now be added or subtracted in the usual way.
- Multiplication of a Decimal Fraction By a Power of 10: Shift the decimal point to the right by as many places as is the power of 10.
Thus, 5.9632 x 100 = 596.32; 0.073 x 10000 = 730.
- Multiplication of Decimal Fractions: Multiply the given numbers considering them without decimal point. Now, in the product, the decimal point is marked off to obtain as many places of decimal as is the sum of the number of decimal places in the given numbers.
Suppose we have to find the product (.2 x 0.02 x .002).
Now, 2 x 2 x 2 = 8. Sum of decimal places = (1 + 2 + 3) = 6.
.2 x .02 x .002 = .000008
- Dividing a Decimal Fraction By a Counting Number: Divide the given number without considering the decimal point, by the given counting number. Now, in the quotient, put the decimal point to give as many places of decimal as there are in the dividend.
Suppose we have to find the quotient (0.0204 ÷ 17). Now, 204 ÷ 17 = 12.
Dividend contains 4 places of decimal. So, 0.0204 ÷ 17 = 0.0012
- Dividing a Decimal Fraction By a Decimal Fraction: Multiply both the dividend and the divisor by a suitable power of 10 to make divisor a whole number.
Now, proceed as above.
Thus,
|
0.00066
|
=
|
0.00066 x 100
|
=
|
0.066
|
= .006
|
0.11
|
0.11 x 100
|
11
|
- Comparison of Fractions:
Suppose some fractions are to be arranged in ascending or descending order of magnitude, then convert each one of the given fractions in the decimal form, and arrange them accordingly.
Let us to arrange the fractions
|
3
|
,
|
6
|
and
|
7
|
in descending order.
|
5
|
7
|
9
|
Now,
|
3
|
= 0.6,
|
6
|
= 0.857,
|
7
|
= 0.777...
|
5
|
7
|
9
|
Since, 0.857 > 0.777... > 0.6. So,
|
6
|
>
|
7
|
>
|
3
|
.
|
7
|
9
|
5
|
- Recurring Decimal:
If in a decimal fraction, a figure or a set of figures is repeated continuously, then such a number is called a recurring decimal.
n a recurring decimal, if a single figure is repeated, then it is expressed by putting a dot on it. If a set of figures is repeated, it is expressed by putting a bar on the set.
Thus,
|
1
|
= 0.333... = 0.3;
|
22
|
= 3.142857142857.... = 3.142857.
|
3
|
7
|
Pure Recurring Decimal: A decimal fraction, in which all the figures after the decimal point are repeated, is called a pure recurring decimal.
Converting a Pure Recurring Decimal into Vulgar Fraction: Write the repeated figures only once in the numerator and take as many nines in the denominator as is the number of repeating figures.
Thus, 0.5 =
|
5
|
; 0.53 =
|
53
|
; 0.067 =
|
67
|
, etc.
|
9
|
99
|
999
|
Mixed Recurring Decimal: A decimal fraction in which some figures do not repeat and some of them are repeated, is called a mixed recurring decimal.
Eg. 0.1733333.. = 0.173.
Converting a Mixed Recurring Decimal Into Vulgar Fraction: In the numerator, take the difference between the number formed by all the digits after decimal point (taking repeated digits only once) and that formed by the digits which are not repeated. In the denominator, take the number formed by as many nines as there are repeating digits followed by as many zeros as is the number of non-repeating digits.
Thus, 0.16 =
|
16 - 1
|
=
|
15
|
=
|
1
|
; 0.2273 =
|
2273 - 22
|
=
|
2251
|
.
|
90
|
90
|
6
|
9900
|
9900
|
- Some Basic Formulae:
- (a + b)(a - b) = (a2 + b2)
- (a + b)2 = (a2 + b2 + 2ab)
- (a - b)2 = (a2 + b2 - 2ab)
- (a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
- (a3 + b3) = (a + b)(a2 - ab + b2)
- (a3 - b3) = (a - b)(a2 + ab + b2)
- (a3 + b3 + c3 - 3abc) = (a + b + c)(a2 + b2 + c2 - ab - bc - ac)
- When a + b + c = 0, then a3 + b3 + c3 = 3abc.
- Laws of Indices:
- am x an = am + n
am
|
= am - n
|
an
|
- (am)n = amn
- (ab)n = anbn
a
|
n
|
=
|
an
| ||
b
|
bn
|
- a0 = 1
Surds:
Let a be rational number and n be a positive integer such that a(1/n) = a
Then, a is called a surd of order n.
- Laws of Surds:
- a = a(1/n)
- ab = a x b
- (a)m = am
Square of numbers in 100
> Choose a number over 100 (START WITH SMALLER NUMBER).
> The last two places will be the square of
the last two digits (keep if any carry) _ _ _ X X.
> The first three places will be the number plus
the last two digits plus any carry: X X X _ _.
Here is an Example:
> let the number be 108:
2. Square the last two digits (no carry): 8 × 8 = 64: _ _ _ 64
3. Add the last two digits to the number: 108 + 08= 116:
so 1 1 6 _ _
4. So 108 × 108 = 11664.
Steps to find square of numbers in 200's
> Choose a number in the 200s (start with numbers under 210, then try for larger ones).
>The first digit of the square is 4: 4 _ _ _ _
> The next two digits will be 4 times the last 2 digits: _ X X _ _
> The last two places will be the square of the last digit: _ _ _ X X
here we take an Example:
> let the number be 207:
> Choose a number in the 200s (start with numbers under 210, then try for larger ones).
>The first digit of the square is 4: 4 _ _ _ _
> The next two digits will be 4 times the last 2 digits: _ X X _ _
> The last two places will be the square of the last digit: _ _ _ X X
here we take an Example:
> let the number be 207:
> The first digit is 4
so 4 _ _ _ _
> The next two digits are 4 times the last digit:
4 × 7 = 28
so _ 2 8 _ _
Square the last digit: 7× 7 = 49
so _ _ _ 49
So finally we get 206 × 206 = 42849.
and For larger numbers work right to left:
> Square the last two digits (keep the carry): _ _ _ X X
> 4 times the last two digits + carry: _ X X _ _
> Square the first digit + carry: X _ _ _ _
example
>If the number to be squared is 225:
> Square last two digits (keep carry):
25x25 = 625 (keep 6): _ _ _ 2 5
> 4 times the last two digits + carry:
4x25 = 100; 100+6 = 106 (keep 1): _ 0 6 _ _
> Square the first digit + carry:
2x2 = 4; 4+1 = 5: 5 _ _ _ _
> So 225 × 225 = 50625.
for this example 37:
> Look for the nearest 10 boundary
> In this case up 3 from 37 to 40.
> Since you went UP 3 to 40 go DOWN 3 from 37 to 34.
> Now mentally multiply 34x40
> The way I do it is 34x10=340;
> Double it mentally to 680
> Double it again mentally to 1360
> This 1360 is the FIRST interim answer.
> 37 is "3" away from the 10 boundary 40.
> Square this "3" distance from 10 boundary.
> 3x3=9 which is the SECOND interim answer.
> Add the two interim answers to get the final answer.
> Answer: 1360 + 9 = 1369
> Look for the nearest 10 boundary
> In this case up 3 from 37 to 40.
> Since you went UP 3 to 40 go DOWN 3 from 37 to 34.
> Now mentally multiply 34x40
> The way I do it is 34x10=340;
> Double it mentally to 680
> Double it again mentally to 1360
> This 1360 is the FIRST interim answer.
> 37 is "3" away from the 10 boundary 40.
> Square this "3" distance from 10 boundary.
> 3x3=9 which is the SECOND interim answer.
> Add the two interim answers to get the final answer.
> Answer: 1360 + 9 = 1369
Square of 3 digit number
LET THE NUMBER BE ABC
SQ (ABC) is calculated like this
STEP 1. Last digit = last digit of SQ(C)
SQ (ABC) is calculated like this
STEP 1. Last digit = last digit of SQ(C)
STEP 2. Second Last Digit = 2*B*C + any carryover from STEP 1.
STEP 3. Third Last Digit 2*A*C+ Sq(B) + any carryover from STEP2.
STEP 4. Fourth last digit is 2*A*B + any carryover from STEP 3.
STEP 5 . In the beginning of result will be Sq(A) + any carryover
from Step 4.
EXAMPLE:
SQ (431)
STEP 1. Last digit = last digit of SQ(1) =1
STEP 2. Second Last Digit = 2*3*1 + any carryover from STEP1.= 6
STEP 3. Third Last Digit 2*4*1+ Sq(3) + any carryover from STEP
2.= 2*4*1 +9= 17. so 7 and 1 carryover
STEP 4. Fourth last digit is 2*4*3 + any carryover (which is 1) . =
24+1=25. So 5 and carry over 2.
STEP 5 . In the beginning of result will be Sq(4) + any carryover
from Step 4. So 16+2 =18.
So the result will be 185761.
SQUARING THE NUMBERS:
1. Squaring the numbers ending with 5.
352 =
Ø Separate the 5 from the digits in front. in this case there is only a 3 in front of the 5. Add 1 to 3 get 4 (3+1= 4)
Ø Multiply these numbers together: 3 x 4 = 12
Ø Write the square of 5 (25) after 12. We will get 1225.
135 2 = ??
Ø Take 13, add 1 to it we will get 14.
Ø Then 13 x 14 = 182
Ø Add the square of 5 next to it. We will get 18225.
SQUARING THE NUMBERS NEAR TO 50:
1. 462 =
Ø Forty six squared means 46 x 46. Rounding upwards, 50 x 50 = 2500.
Ø Take 50 and 2500 as our reference points.
50 462
- 4
46 = 50-4, so 4 is a minus number.
Ø So we take 4 from the 25 hundreds.
Ø (25-4) x 100= 2100
Ø To get the rest of the answer, we square the number in the minus. ( 4 2= 16)
Ø Add 2100 and 16 we will get 2116 is the answer.
562 =
Ø Fifty six squared means 56 x 56. Rounding upwards, 50 x 50 = 2500.
Ø Take 50 and 2500 as our reference points.
50 562
+6
56 = 50+4, so 6 is a positive number.
Ø So we add 6 to 25 hundreds.
Ø (25+6) x 100= 3100
Ø To get the rest of the answer, we square the number in the minus. ( 62= 36)
Ø Add 3100 and 36 we will get 3136 is the answer.
SQUARING NUMBERS NEAR TO 500:
Ø This is similar to our strategy for squaring numbers near 50.
Ø Five hundred times 500 is 250000, we take 500 and 250000 as our reference number.
1. 5062 =
500 5062
+6
5002 = 250000
Ø Five hundred and six is greater than 500,
Ø Square of 500 is 250000
Ø The number 6 is added to the thousands
Ø (250+6) x1000 = 256000
Ø Square 6 is 36.
Ø 256000+36 =256036 is the answer.
Square the number ends with 1:
1. 312 =
Ø First, subtract 1 from the number. The number now ends in zero and should be easy to square. (302 = 3 x 3 x 10 x 10) = 900
Ø Add 30 and its next number 31 (30+31). We will get 61)
Ø Add (900 + 61) = 961.
2. 3512=?
Ø 3502 = 122500
Ø 350 +351 = 701
Ø 122500 +701 = 123201
WE CAN ALSO USE THE METHOD FOR SQUARING NUMBERS ENDING IN 1 FOR THOSE ENDING IN 6.
3. 862 =
Ø 852 =7225
Ø 85+86 = 171
Ø 7225+171 = 7396
Squaring numbers ending with 9
1. 292 =
Ø Add 1 to the number. The number now ends in zero and is easy to square.
Ø 302 = 900
Ø Now add 30 with given number29 (30+29 =59)
Ø Then sub (900 - 59 = 841)
2. 3492 =
Ø 3502 = 122500
Ø 350+349 = 699
Ø Sub (122500 - 699 = 121801)
Square a 2 Digit Number Ending in 5
For this example we will use 25
• Take the "tens" part of the number (the 2 and add 1)=3
• Multiply the original "tens" part of the number by the new number (2x3)
• Take the result (2x3=6) and put 25 behind it. Result the answer 625.
Try a few more 75 squared ... = 7x8=56 ... put 25 behind it is 5625.
55 squared = 5x6=30 ... put 25 behind it ... is 3025. Another easy one! Practice it on paper first!
SINGLE STEP:
35 square
(3x[3+1]) / (5x5) = 12 / 25 = 1225
(3x[3+1]) / (5x5) = 12 / 25 = 1225
Square 2 Digit Number: UP-DOWN Method
Square a 2 Digit Number, for this example 37:
• Look for the nearest 10 boundary
• In this case up 3 from 37 to 40.
• Since you went UP 3 to 40 go DOWN 3 from 37 to 34.
• Now mentally multiply 34x40
• The way I do it is 34x10=340;
• Double it mentally to 680
• Double it again mentally to 1360
• This 1360 is the FIRST interim answer.
• 37 is "3" away from the 10 boundary 40.
• Square this "3" distance from 10 boundary.
• 3x3=9 which is the SECOND interim answer.
• Add the two interim answers to get the final answer.
• Answer: 1360 + 9 = 1369
ADDITION
The basic rule for mental addition:
To add 9, add 10 and subtract 1: to add 8, add 10 and subtract 2; to add 7 add 10 and subtract 3, and so on.
Ø If you wanted to add 47, you would add 50 and subtract 3,
Ø To add 196, add 200 and subtract 4.
Ø To add 38 to a number, add 40 and subtract 2,
TWO DIGIT MENTAL ADDITIONS:
If the unit’s digit is high, round off to the next ten and then subtract the difference. If the units’ digit is low, add the tens then the units.
Ø With two digit mental addition you add the tens digit of each number first, then the units. If the unit’s digit is high, round off the number upwards and then subtract the difference. If you are adding47, add 50, and then subtract 3.
Ø To add 35, 67, and 43 together you would begin with 34, add 70 to get 105, subtract 3 to get 102, add 10 to get 142 then the 3 to get your answer of 145.
ADDING THREE DIGIT NUMBERS:
355+752+694 =?
Ø 355+700 = 1055
Ø 1055+50+2 = 1107
Ø 1107+700-6 = 1807-6 = 1801
OR
Ø You may prefer to add from left to right; adding the hundreds first, then the tens and then the units.
ADDITING LARGER NUMBERS:
8461
Ø We begin with the thousands column.8+5 = 13, since we are dealing with thousands, our answer is 13 thousand.
Ø Observe that the numbers in the hundreds column conveniently add to 10, so that gives us another thousand. Then answer is 14000.
Ø Then add 61 to 14000, we getting 14061.
Ø Add 80 to and subtract 2. To add 80 add 100 and subtract 20, (14061+100-20-2) = 14161-20-2=14141-2=14139 is the answer.
Ø An easy rule is: when adding a column of numbers add pairs of digits to make tens first, then add the other digits.
SUBTRACTION:
To subtract mentally, try and round off the number you are subtracting and then correct the answer.
To subtract 9, take 10 and add 1: to subtract 8, take 10 and add 2; to subtract 7, take 10 and add 3,
1. Eg: 56-9 =
-1
(To take 9 from 56 in your head, the easiest and fastest method is to subtract 10, (46) and add1 we get 47.)
2. 54-38 = 16
+2
Ø 44-40, plus 2 makes 16
3. 436-87 =
+13
Ø Take 100 to get 336. Add 13 and we will get 349 easy.
Ø SUBTRACTING ONE NUMBER BELOW A HUNDREDS VALUE FROM ANOTHER WHICH IS JUST ABOVE THE SAME HUNDREDS NUMBERS.
THREE DIGIT SUBTRACTIONS:
1. 461 -275 =
25
161+25 = 160+20+5+1 = 186
2. 834 – 286 =
14
534+14 = 530+10+4+4 = 540+8 = 548
SUBTRACTION METHOD ONE:
1. 7254-3897 =
3 3 5 7
Ø Subtract 7 from 4. We can’t, so we borrow 1 from the tens column.
Ø Cross out the 5 and write 4.
Ø Don’t say 7 from 14, we have to say 7 from 10 and add 4 we getting 3+4 = 7 ( the first digit of the answer)
Ø Nine from 4 won’t go, so borrow again. Nine from 10 is 1, plus 4, the next digit answer.
Ø Eight from 1 won’t go, so borrow again. Eight from 10 is 2, plus 1 is 3, three from 6 is 3, the final digit of the answer.
SUBTRACTION METHOD TWO:
Ø Subtract 7 from 4. We can’t, so we borrow 1 from the tens column. Put a 1 in front of the 4 to make 14 and write a small 1 alongside the 9 in the tens column. Don’t say 7 from 14, but 7 from 10, add 4 on top gives 7, the first digit of the number.
Ø Ten ( 9+1) from 5 won’t go so borrow again in a similar fashion. Ten from 15 is 5 or 10 is zero, plus 5 is 5.
Ø Nine from 2 won’t go, so borrow again. Nine from 10 is 1 plus 2 is 3.
Ø Four from 7 is 3. You have your answer.
SUBTRACTION FROM A POWER OF 10:
The rule is : SUBTRACT THE UNITS DIGIT FROM 10, THEN EACH SUCCESSIVE DIGIT FROM 9, THEN SUBTRACT 1 FROM THE DIGIT ON THE LEFT.
1. 1000
-574
Ø 10-4=6,
Ø 9 - 7 = 2,
Ø 9 - 5 = 4,
Ø 1 - 1 = 0
The answer is 0426
SUBTRACTING SMALLER NUMBERS:
If the number we are subtracting has fewer digits than the one you are subtracting from, then add zeros before the number (at least, mentally) to make the calculation:
For instance:
23 000 – 46 =
23 000
22 954
Use the same principle as subtraction method 2.
SHORTCUT FOR SUBTRACTION
Ø What is the easiest way to take 90 from a number?
Take 100 and give back 10
Ø What is the easiest way to take 80 from a number?
Take 100 and give back 20
Ø What is the easiest way to take 70 from a number?
Take 100 and give back 30
-2 35 30
Ø How do we take 70 from 13,330?
Ø Take away 100 and give back 30
Kerala SSLC Exam 2014 Results Published
>> SSLC Exam results of Kerala have been announced by the Education Department on 16 April 2014.
>> As many as 4.42 lakh students have been declared eligible for higher studies in the SSLC examinations, the results of which were announced in a record 19 days.
>> The success rate in 2014 touched 95.47 per cent, an increase of 1.3 percentage points over the last year’s figure. Success rate among boys this year was 94.44 per cent. It was 96.53 per cent among girls.
>> This year, 14,802 students secured A+ in all subjects, 4,729 more than the corresponding figure for 2013. Last year, 10,073 students secured A+ in all subjects.
>> The ‘Save A Year’ (SAY) examination for those who gained eligibility for higher studies would be held at select centres from May 12 to 17. Applications for this could be submitted from April 24 to 28 to the respective headmasters. Applications for photocopy, revaluation, and scrutiny of the answer sheets may be submitted online from April 24 to 28 till 1 p.m. The certificates of the students will be made available at the District Education Office concerned by May 15.
View Results from following links
IMPORTANT INSTRUCTIONS FOR PA SA EXAM CANDIDATES
1. Candidates are requested to appear for the written test at the Centre on the date and time specified. Candidate should reach the test centre 60 minutes before the commencement of the examination. Candidates are permitted up to 15 Minutes after the commencement of the examination but however they are not permitted any extended time.
2. Maximum candidates have been accommodated at the Examination City of their Preference 1. However their Preference 2 and 3 have been also have been kept in view keeping the volume of candidates appearing in the examination and in the exigencies.
3. No change of Test Centre/test date and address of correspondence will be entertained.
4. Bring this Admit Card in ORIGINAL to the examination centre. Keep a photocopy of the Admit Card with you for future reference. You are required to put your Signatures on this Admit Card in the given box ONLY in the presence of Invigilator in the examination hall and it will be collected during the examination.
5. Admit Card is displayed only on the website www.pasadrexam2014.in Check your particulars in the Admit Card carefully. Discrepancy, if any,
should be immediately reported to the mail admitcardhelpdesk.dopexam@gmail.com Relevant corrections, if any and accepted, will be made to your On-Line Admit Card and the same can be Downloaded from the website again.
6. Admit Cards will not be issued at the Examination Centre under any circumstances. Printout of Downloaded Admit Card from the website www.pasadrexam2014.in are valid. Candidates will not be permitted without valid admit card.
7. Please ensure that you bring only ball point pen of colour Black or Blue for marking the OMR Answer Sheet. Marking with “gel” or any other type of pen is NOT allowed.
8. Answer Sheet is of OMR (Optical Mark Recognition) type. For every question there is only one Correct Option. Darken the appropriate Circle to indicate the Correct Answer. Please note No Change is permissible once marked. Applicant who darken more than one circle for any question can’t be valued and rejected. DO NOT put any stray marks anywhere on theanswer sheet. Rough work may be done on the blank space in your question booklet. There is “No Negative Marking”.
9. OMR answer sheet has two copies. Do Not separate them. Impressions marked on the Original Sheet will automatically get transferred to the Copy. Original copy will be used for Result Processing. After completion of exam & before leaving the examination hall Candidate is to handover the ORIGINAL copy to the invigilator and candidate may retain Carbonless Copy. It is the responsibility of the candidate to handover the ORIGINAL OMR Sheet to the room invigilator before leaving the examination hall. Question Booklet is allowed to be retained by the candidate.
10. Candidates are likely to undergo searching/ frisking at the entrance of the exam centre. Please cooperate.
11. MOBILE PHONES/SCANNING DEVICES/ANY ELECTRONIC GADGET/ WEAPONS / FIRE ARMS are strictly prohibited inside the examination centre. Examination centre will not be responsible for its safety/loss. There is no arrangement made for securing your valuables.
12. Impersonation and/or possession of any material, electronic equipment even remotely connected or adverse to proper conduct and performance of the examination may render a candidate liable to be expelled from the Examination Hall and/or cancellation of candidature apart from any other punishment/penalty that may be imposed upon the candidate.
13. Candidates are not allowed to carry any papers, note books, books, calculators, etc. into the examination hall. Any candidate found using or in possession of such unauthorized material or indulging in copying or adopting unfair means will be summarily disqualified.
14. The duration of Paper is 120 minutes. The syllabus for the Paper I is already furnished in the Notification & FAQ on website.
15. Result of successful candidates in this Paper–I shall be published on the website. Candidate is advised to regularly visit the web site www.pasadrexam2014.in for ascertaining updates.
16. The candidature for this test is PROVISIONAL and is subject to fulfilling the education and other eligibility criteria as prescribed in the Notification/Advertisement advertised in the newspaper & also at the website www.pasadrexam2014.in. If Candidate is found ineligible at a later date his/her candidature will be summarily rejected. Mere appearing OR qualifying in the test does not confer any right on the applicant for claiming selection.
17. Visually Impaired (PH - I) candidate is requested to bring “Scribe” at his /her own cost. The scribe should read the Questions in low voice and mark the options as told by the candidate. It should not disturb other candidates in the room. Any misconduct by the scribe/ or candidate himself shall be treated to have been done by that candidate and shall lead to cancellation of the candidature of the candidate. Visually Impaired (PH - I) candidate will allowed 40 minutes compensatory (extra) time for completing the examination.
18. Canvassing in any form by the candidate would entail his/her disqualification.
19. Candidate will not be allowed to leave the examination hall till the examination is over.
20. Please read the instructions carefully on Question Booklet & OMR Sheet. The candidate should fill up all the particulars on the OMR Answer sheetlegibly before starting to answer the questions.
21. Decision of the Department of Posts in respect of all matters pertaining to this recruitment test would be final and binding on all the Applicants/Candidates.


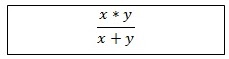

No comments:
Post a Comment